Overview of CUQIpy

Overview of CUQIpy#

Table of Contents:#

Note: some of the details mentioned here will make more sense after going through the next notebook that demonstrates how to use CUQIpy to solve a simple Bayesian inverse problem.

What is CUQIpy? #

  • CUQIpy is a Python package.

  • CUQIpy stands for Computational Uncertainty Quantification for Inverse Problems in Python.

  • CUQIpy provides a framework for solving inverse problems using Bayesian inference.

  • The framework enables:

    • Modeling Bayesian inverse problems

    • Solving Bayesian inverse problems using classical and advanced numerical tools

    • Analyzing the solution of Bayesian inverse problems

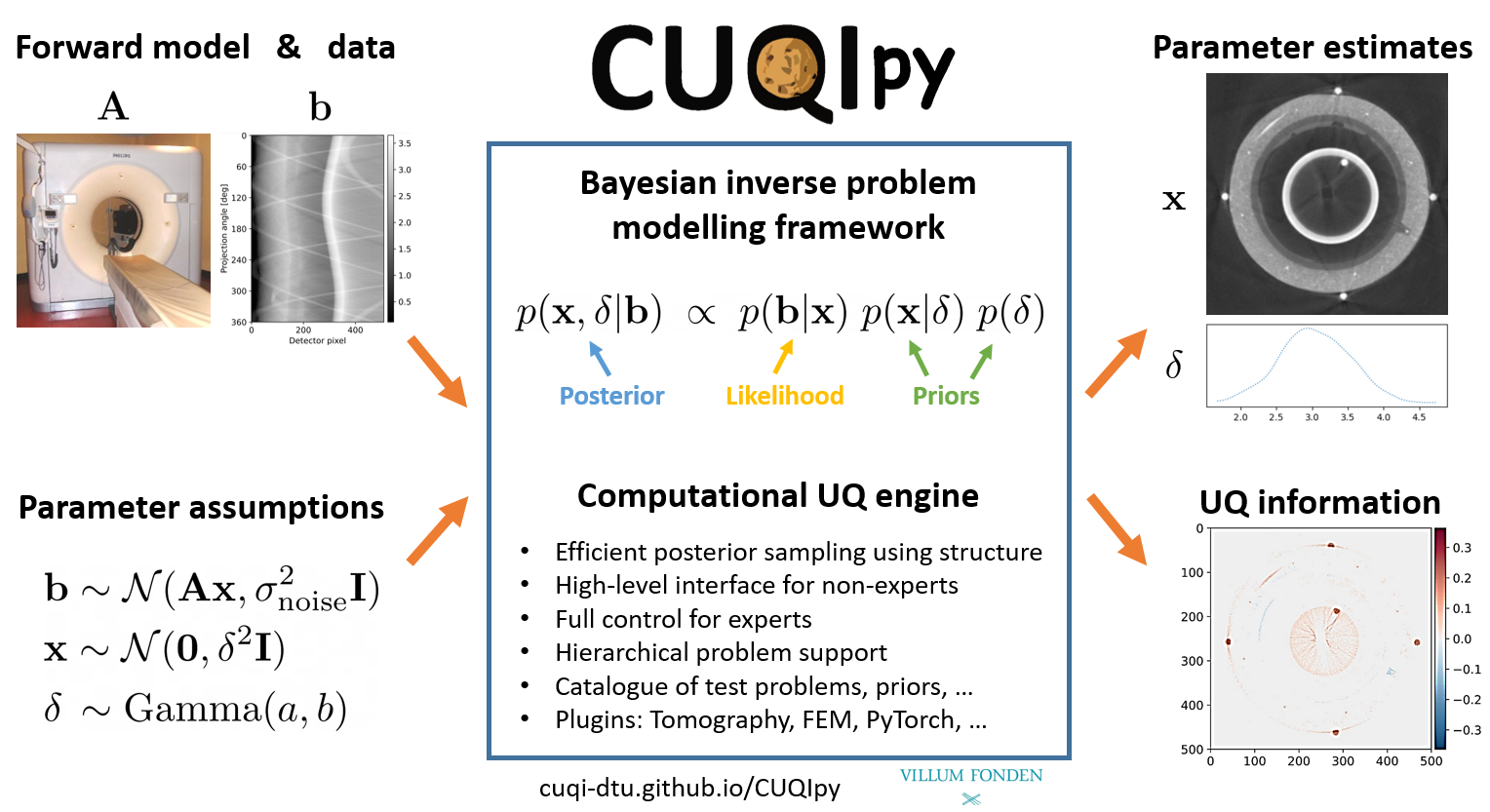
CUQIpy overview

Why CUQIpy? #

CUQIpy is built to address the need for:

  • A unified framework for solving Bayesian inverse problems across various scientific and engineering applications

  • A platform for modeling, solving and analyzing the solution of Bayesian inverse problems

  • A tool that can be used for both research and teaching

  • A tool that can be used by both beginners and advanced users

  • A tool that combines classical and advanced and scalable numerical methods for solving Bayesian inverse problems

  • A tool that is implemented purely in Python with minimal dependencies and can be easily maintained and integrated with other tools

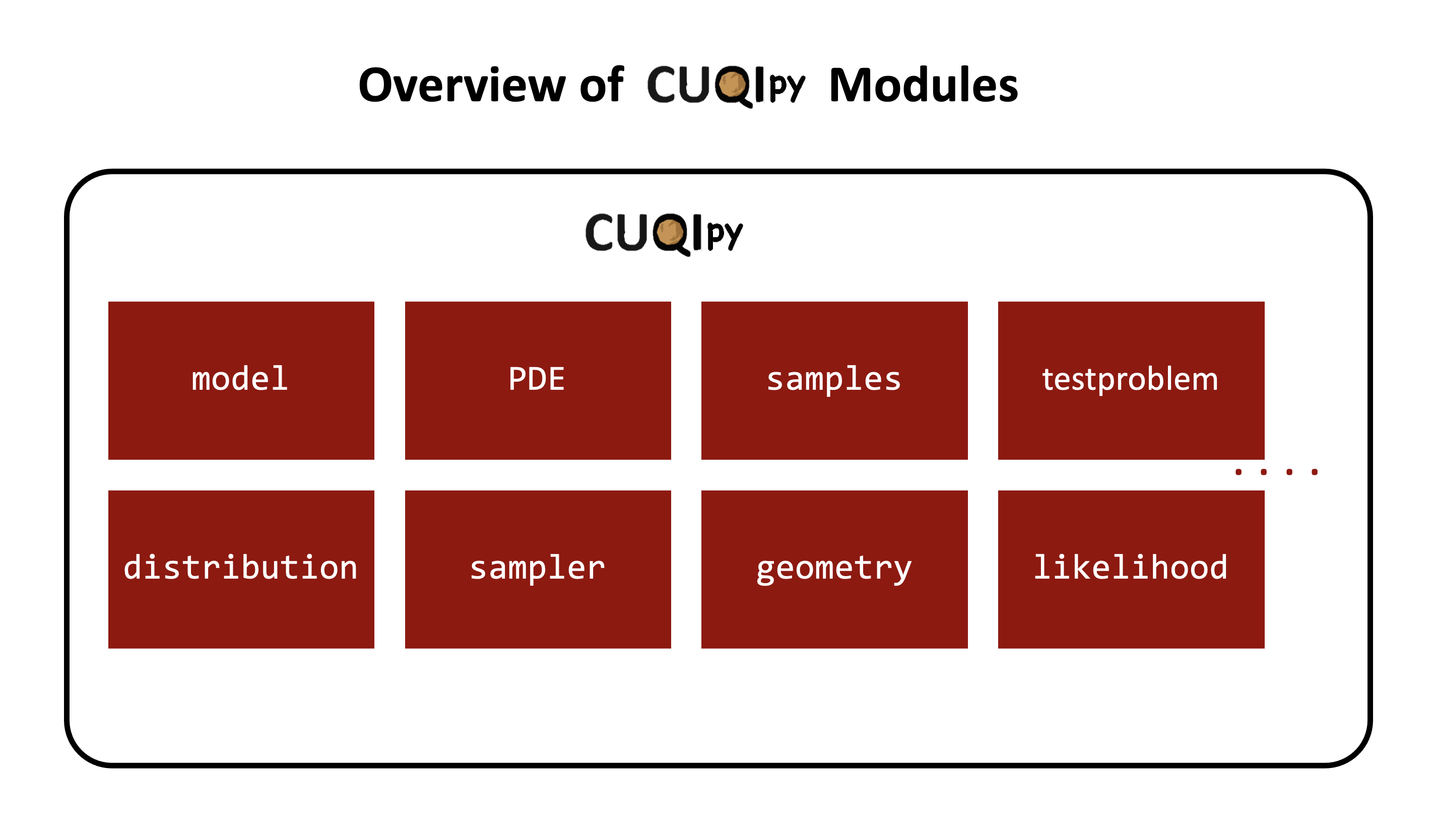
CUQIpy modules #

  • CUQIpy consists of many modules for modeling, solving, and analyzing Bayesian inverse problems.

  • These modules mostly correspond to typical components/tools needed for modeling and solving Bayesian inverse problems.

  • Each module contains classes and functions that are used to perform specific tasks.

  • Click here for an overview of the modules available in CUQIpy.

CUQIpy modules

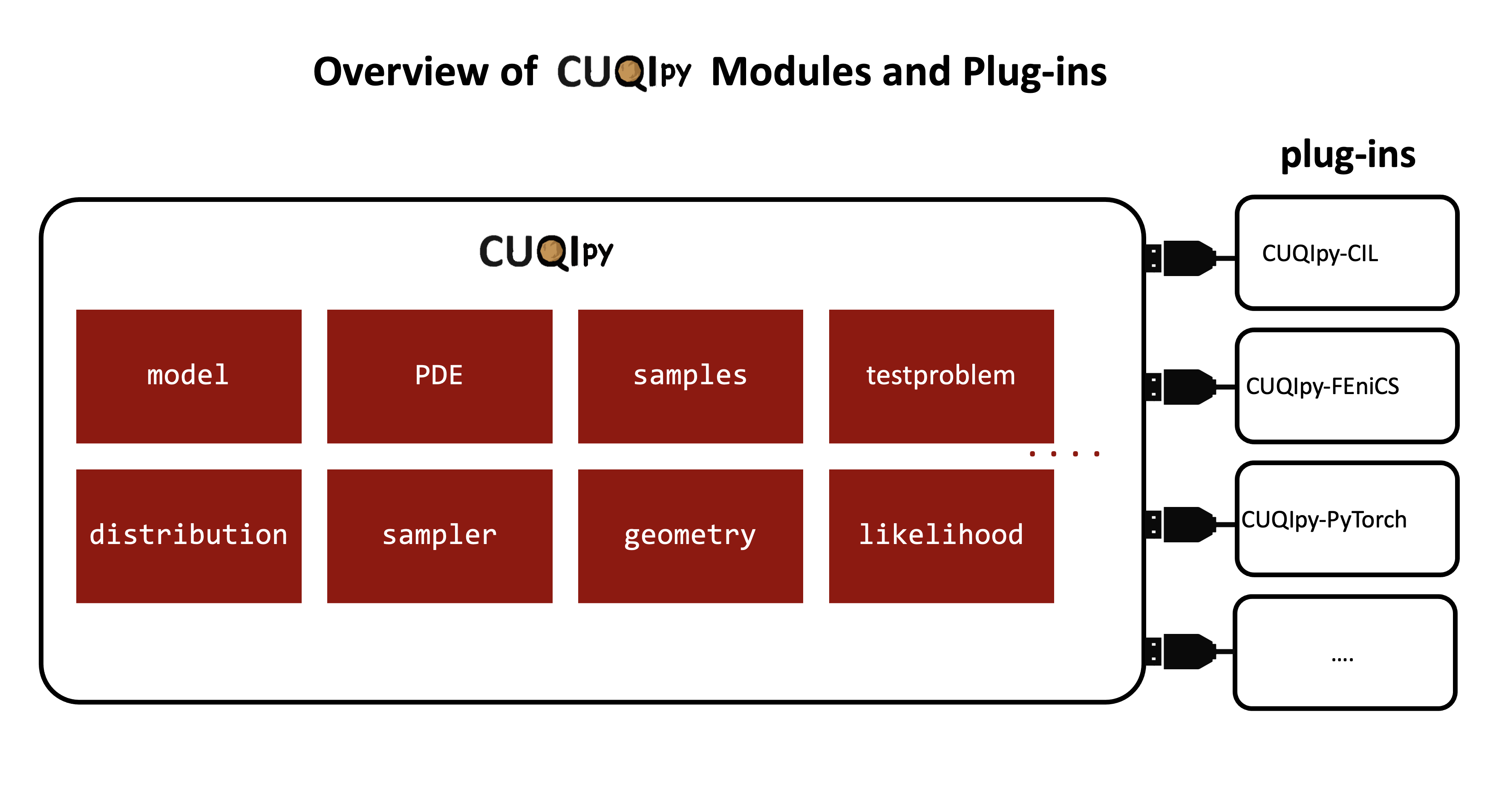
CUQIpy plugins #

  • In addition to the CUQIpy modules, CUQIpy also has plugins that extend the functionality of the framework.

  • These plugins allow integration of third-party software and tools with CUQIpy.

  • Click here to see the list of plugins available in CUQIpy.

CUQIpy plugins

CUQIpy design principles #

  • Provide simple and intuitive interface for users

  • Design for flexibility, extensibility, modularity, and maintainability

  • Accommodate both beginners and advanced users. e.g.,

    • Provide a set of test problems to use for experimentation and prototyping

    • Automatic sampler selection for a range of problems

    • Enable advanced customization of the problem setup and solution

  • Aligning the modeling code with the mathematical formulation of the problem, e.g.,

Bayesian model:

\[\begin{split} \begin{align*} d &\sim \text{Gamma}(1, 10^{-4})\\ s &\sim \text{Gamma}(1, 10^{-4})\\ x &\sim \text{LMRF}(\mathbf{0}, d^{-1})\\ y &\sim \text{Gaussian}(\mathbf{A}\mathbf{x}, s^{-1}\mathbf{I})\\ p(d,s,x,y) &= p(d)p(s)p(x|d)p(y|x,s) \end{align*} \end{split}\]

where \(d^{-1}\) and \(s\) are the precision parameters of the prior (the LMRF) and the data distribution (the Gaussian), respectively, \(x\) is the unknown parameter, and \(y\) is the data. \(\mathbf{A}\) is the forward operator.

Bayesian model in CUQIpy:

d = Gamma(1, 1e-4)
s = Gamma(1, 1e-4)
x = LMRF(0, lambda d: 1/d)
y = Gaussian(A@x, lambda s: 1/s)
joint = JointDistribution(d, s, x, y)

See setting up a Bayesian model in CUQIpy in 4 steps here.

CUQIpy team #

Contents