Two forward models

Two forward models#

We introduce here two forward models: 1D Poisson and 1D convolution. We will use these forward models in the book to apply and demonstrate various concepts in Bayesian inversion.

Contents of this notebook: #

Learning objectives: #

  • Create (or load pre-existing) linear and non-linear forward models in CUQIpy and use them

  • Create and plot input for the forward models and compute and plot the corresponding output

  • Mathematically define two forward models: 1D Poisson and 1D Convolution and use them in CUQIpy

Hide code cell content 
from cuqi.testproblem import Poisson1D, Deconvolution1D, Heat1D
from cuqi.distribution import Gaussian
from cuqi.array import CUQIarray
import numpy as np
import matplotlib.pyplot as plt

Forward model: 1D Poisson #

Consider a heat conductive rod of length \(L = \pi\) with a varying conductivity (the conductivity of the rod changes from point to point). We fix the temperature at the end-points of the rod and apply a heat source distributed along the length of the rod. We wait until the rod reaches an equilibrium temperature distribution. The equilibrium temperature of the rod is modelled using the second order steady-state PDE as

\[\begin{split} \left\{ \begin{aligned} & \dfrac{\dd}{\dd \xi}\left(u(\xi) \dfrac{\dd y(\xi)}{\dd \xi}\right) = -f(\xi), \quad & \xi\in (0,L) \\ & y(0) = y(L) = 0. \end{aligned} \right. \end{split}\]

Here, \(y\) represents the temperature distribution along the rod, \(u(\xi) \) is the unknown conductivity of the rod and \(f(\xi)\) is a deterministic heat source given by

\[ \begin{aligned} f(\xi) = 10\exp( -\frac{ (\xi - L/2)^2} {0.02} ). \end{aligned} \]

To ensure that the conductivity of the rod is non-negative, we parameterize \(u\) by a random variable \(x\) as follows:

\[ \begin{aligned} u( \cdot ) = \exp( x( \cdot ) ) \end{aligned} \]

where \(x\) is not necessarily positive.

Let us load the forward model that maps the random variable \(x\) to the temperature distribution \(y\) in CUQIpy. We will use the following parameters:

  • dim : number of discretization points for the rod

  • L : length of the rod

  • f : a function that represents the heat source

dim = 128
L = np.pi
f = lambda xi: 10*np.exp(-(xi-L/2)**2 / 0.02)

Then we can load the 1D Poisson forward model as follows:

A = Poisson1D(dim=dim, endpoint=L, source=f).model

We print the forward model to see its details.

A

CUQI PDEModel: Continuous1D(128,) -> Continuous1D(127,).
    Forward parameters: ['x'].
    PDE: SteadyStateLinearPDE.

We can look at the domain and range geometries of the forward model.

print(A.domain_geometry)
print(A.range_geometry)

Continuous1D(128,)
Continuous1D(127,)

These geometries are of type Continuous1D which represents a 1D continuous signal/field defined on a grid. We can view the grid:

print(A.domain_geometry.grid)

[0.         0.02473695 0.0494739  0.07421085 0.0989478  0.12368475
 0.1484217  0.17315865 0.1978956  0.22263255 0.2473695  0.27210645
 0.2968434  0.32158035 0.3463173  0.37105425 0.3957912  0.42052815
 0.4452651  0.47000205 0.494739   0.51947595 0.5442129  0.56894985
 0.5936868  0.61842375 0.6431607  0.66789765 0.6926346  0.71737155
 0.7421085  0.76684545 0.7915824  0.81631935 0.8410563  0.86579325
 0.8905302  0.91526715 0.9400041  0.96474105 0.989478   1.01421495
 1.0389519  1.06368885 1.0884258  1.11316275 1.1378997  1.16263665
 1.1873736  1.21211055 1.2368475  1.26158445 1.2863214  1.31105835
 1.3357953  1.36053225 1.3852692  1.41000615 1.4347431  1.45948005
 1.484217   1.50895395 1.5336909  1.55842785 1.5831648  1.60790175
 1.6326387  1.65737565 1.6821126  1.70684955 1.7315865  1.75632345
 1.7810604  1.80579735 1.8305343  1.85527125 1.8800082  1.90474515
 1.9294821  1.95421905 1.978956   2.00369295 2.0284299  2.05316685
 2.0779038  2.10264075 2.1273777  2.15211465 2.1768516  2.20158855
 2.2263255  2.25106245 2.2757994  2.30053635 2.3252733  2.35001025
 2.3747472  2.39948415 2.4242211  2.44895805 2.473695   2.49843195
 2.5231689  2.54790585 2.5726428  2.59737975 2.6221167  2.64685365
 2.6715906  2.69632755 2.7210645  2.74580145 2.7705384  2.79527535
 2.8200123  2.84474925 2.8694862  2.89422315 2.9189601  2.94369705
 2.968434   2.99317095 3.0179079  3.04264485 3.0673818  3.09211875
 3.1168557  3.14159265]

Additionally, the properties domain_dim and range_dim of the forward model represent the dimension of the input and output of the forward model, respectively.

print(A.domain_dim)
print(A.range_dim)

128
127

Let us create an array representing a constant conductivity over the grid nodes

some_x_array = 20*np.ones(A.domain_dim)

We can wrap the array in a CUQIarray object which is the main data structure in CUQIpy for variables (e.g. arrays and fields)

some_x = CUQIarray(some_x_array, geometry=A.domain_geometry)

Note that we pass geometry=A.domain_geometry to equip the CUQIarray object with the same geometry as the domain of the forward model, which is has information about what the values of the array represent (e.g. function values on a grid for this case).

We can plot the conductivity array using the plot method of the CUQIarray object

some_x.plot()

[<matplotlib.lines.Line2D at 0x7f88f8e61d20>]
../_images/bdaab509899c514f692403f6205b42db57736843a0888d413058a783d6abe149.png

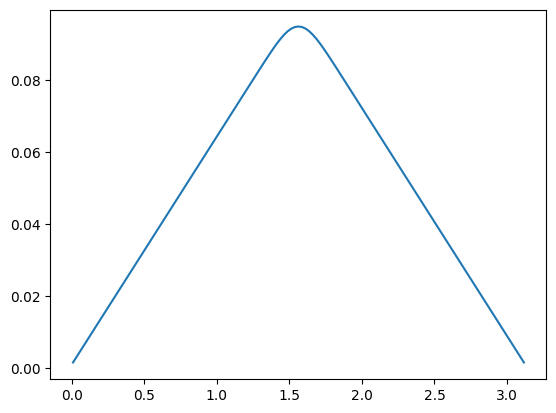
We can also evaluate the forward model at the conductivity array and plot the solution:

some_y = A(some_x)
some_y.plot()

[<matplotlib.lines.Line2D at 0x7f88f8d4a950>]
../_images/6e6b0df0dac52968bb93b95d276763f2518c7b2e576c7f6e549ce88ffa2946b6.png

Exercise: #

  • Is this true for you: “I can, mathematically, write a definition of a 1D Poisson forward model that maps the conductivity field to the temperature distribution field”? If not, what questions do you have?

  • Trying a different conductivity profile:

    • Create another constant conductivity profile another_x of value 20 as a CUQIarray object.

    • Evaluate the forward model at the new conductivity profile and store the result in a variable another_y. Plot the solution.

    • In one plot, compare the solutions some_y and another_y using the plot method of the CUQIarray object. What do you observe? and why?

  • Experimenting with setting up the map in Poisson1D:

    • Execute help(Poisson1D)

    • Note the map parameter of Poisson1D. We can use this parameter to transform the conductivity field before solving the PDE. Create the forward model again, name it A_map, with setting up map to be lambda x: np.exp(x) to ensure that the conductivity is always positive.

    • Inspect the domain and range geometries of the new forward model A_map what is different this time, and why?

    • Create a CUQIarray object x_with_map with a constant conductivity profile of value 0 and evaluate the forward model at x_with_map and store it in variable y_with_map. Make sure to use the right geometry for x_with_map.

    • Plot x_with_map using x_with_map.plot(), What do you observe?

    • Plot the solution y_with_map and some_y in the same plot. What do you observe? and why?

  • Experimenting with setting up the field_type in Poisson1D:

    • Note the field_type parameter of Poisson1D. We can use this parameter to change the parameterization of the conductivity field. Create the forward model again, name it A_step, with setting both the map as in the previous exercise and the field_type to be "Step" to generate a step parameterization of the conductivity field.

    • What is the domain and range geometries of the new forward model A_step?

    • Create x_step to be x_step = CUQIarray(np.arange(A_step.domain_dim)*0.1, geometry=A_step.domain_geometry).

    • Plot x_step using x_step.plot().

    • What does the dimension A_step.domain_dim represent? and is it equal to the size of the domain geometry grid?

    • Evaluate the forward model at x_step and store it in variable y_step. Plot the solution.

  • Is this true for you: “I can load the pre-existing Poisson 1D forward model in CUQIpy and evaluate it on some input and visualize the input and output”? If not, what questions do you have?

# your code here

Forward model: 1D convolution #

The mathematical model for convolution of a random signal on a one-dimensional spatial domain \(D\), can be written as a stochastic Fredholm integral equation of the first kind:

\[ \begin{aligned} y(\xi) = \int_{D} k(\xi,\xi')x(\xi')\,\dd \xi' \end{aligned} \]

where \(y(\xi)\) denotes the convolved signal and we assume a Gaussian convolution kernel. In practice, a finite-dimensional representation of the integral equation is employed. After discretizing the signal domain into \(N\) components, the convolution model can be expressed as a system of linear algebraic equations \(\ve{y}=\mat{K}\ve{x}\).

Let us load the forward model that maps the random variable \(\ve{x}\) to the convolved signal \(\ve{y}\) in CUQIpy. We will use the following parameters to specify the forward model:

  • dim : is the number of discretization points for the signal, \(N\)

  • PSF : a function that represents the point spread function, i.e., the convolution kernel

  • PSF_size : the size of the PSF (less or equal to dim)

  • PSF_param : A parameter of the PSF, the larger the size the more the blur applied to the signal

  • BC : boundary conditions for the convolution

We set the parameters as follows:

dim = 201
PSF = 'gauss' # Gaussian PSF
PSF_size = np.round(dim/3)
PSF_param = np.round(dim/20)
BC='reflect' # Boundary condition

Then we can load the 1D convolution forward model as follows (note that we refer to the forward model as a convolution model which we obtain from the Deconvolution1D test problem, the latter represents the BIP of deconvolving the signal):

A_deconv = Deconvolution1D(dim=dim, PSF=PSF, PSF_size=PSF_size, PSF_param=PSF_param, BC=BC).model

Let us create a function representing a signal that we want to convolve.

signal_function = lambda xi: (xi>np.round(dim*4/10))*(xi<np.round(dim*6/10))

We evaluate the function signal_function at the discretization grid points and wrap it in a CUQIarray object.

signal_array = signal_function(A_deconv.domain_geometry.grid)
signal = CUQIarray(signal_array, geometry=A_deconv.domain_geometry)

Let us plot the signal

signal.plot()

[<matplotlib.lines.Line2D at 0x7f88f8decfd0>]
../_images/15bbd75d0ea8415669d4d1200fdc21260bead9bc17f6c19dd851506c37c719ad.png

Now, we evaluate the forward model at the signal and plot the solution:

A_deconv(signal).plot()

[<matplotlib.lines.Line2D at 0x7f88f8c80910>]
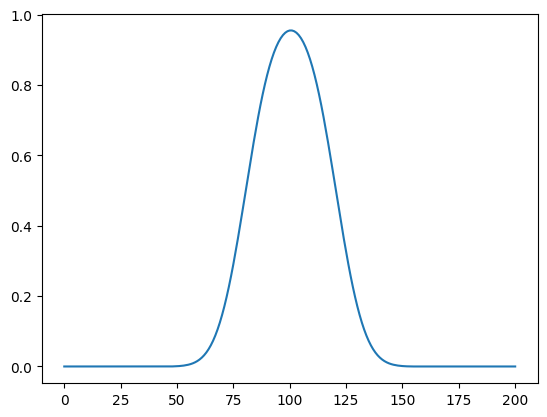
../_images/1ca058da94a0abcbbcd1bd1db6efb09c392df52ed77e7cc412ae6ff7466a59d3.png

We see that the signal is blurred due to applying the convolution operation (the forward model).

Exercise: #

  • Type help(Deconvolution1D) to see the documentation of this test problem.

  • Experimenting with the convolution strength:

    • Create another convolution model B with the same parameters as A_deconv but with a different PSF_param value, use PSF_param=PSF_param/2. Evaluate the forward model B at the signal and plot the solution along with A_deconv(signal) in the same plot. What do you observe?

  • Experimenting with setting up the PSF:

    • Create a new convolution model C with the same parameters as A_deconv but with a different PSF, use PSF=np.ones(m)/m. Evaluate the forward model C at the signal and plot the solution along with A_deconv(signal) in the same plot (try for different values of m: 5, 10, 20). What do you observe?

  • Experimenting with setting up the BC:

    • Create a new convolution model D with the same parameters as A_deconv but with a different BC, use BC="periodic". Evaluate the forward model D at the signal and plot the solution along with A_deconv(signal) in the same plot. What do you observe?

    • Now create another signal another_signal as another_signal = signal + 0.1*np.exp((D.domain_geometry.grid - np.round(dim*7/8))/10). Plot the new signal. Evaluate the forward models A_deconv, and D at the new signal and plot the solutions in the same plot. What do you observe?

  • Is this true for you: “I can load the pre-existing convolution 1D forward model in CUQIpy, experiment with its parameter setup, evaluate it on some input, and visualize the input and output”? If not, what questions do you have?

# your code here
Contents