Note

Go to the end to download the full example code.

Uncertainty Quantification in one-dimensional deconvolution#

This tutorial walks through the process of solving a simple 1D deconvolution problem in a Bayesian setting. It also shows how to define such a convolution model in CUQIpy.

Setup#

We start by importing the necessary modules

import cuqi
import numpy as np
import matplotlib.pyplot as plt

Setting up the forward model#

We start by defining the forward model. In this case, we will use a simple convolution model. The forward model is defined by the following equation:

\[\mathbf{y} = \mathbf{A} \mathbf{x}\]

where \(\mathbf{y}\) is the data, \(\mathbf{A}\) is the convolution (forward model) operator, and \(\mathbf{x}\) is the solution.

The easiest way to define the forward model is to use the testproblem module. This module contains a number of pre-defined test problems that contain the forward model and synthetic data. In this case, we will use the cuqi.testproblem.Deconvolution1D test problem. We extract the forward model and synthetic data from the test problem by calling the get_components() method.

# Forward model and data
A, y_data, info = cuqi.testproblem.Deconvolution1D().get_components()

There are many parameters that can be set when creating the test problem. For more details see the cuqi.testproblem.Deconvolution1D documentation. In this case, we will use the default parameters. The get_components() method returns the forward model, synthetic data, and a ProblemInfo object that contains information about the test problem.

Let’s take a look at the forward model

print(A)

CUQI LinearModel: Continuous1D[128] -> Continuous1D[128].
    Forward parameters: ['x'].

We see that the forward model is a a LinearModel object. This object contains the forward model and the adjoint model. We also see that the domain and range of the forward model are both continuous 1D spaces. Finally, we see that the default forward parameters are set to \(\mathbf{x}\).

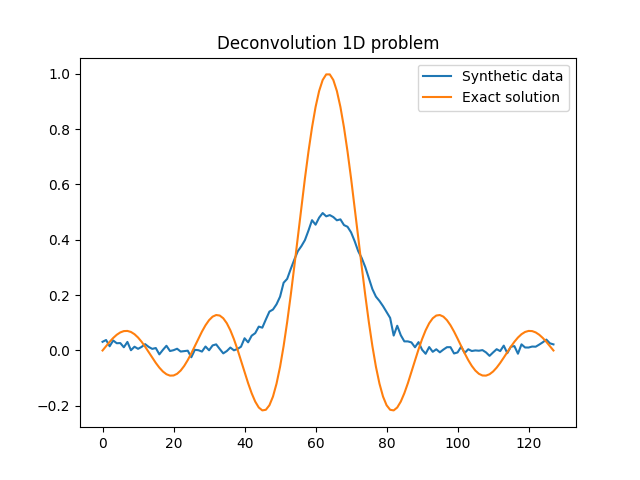
Let’s take a look at the synthetic data and compare with the exact solution that we can find in the ProblemInfo object.

y_data.plot(label="Synthetic data")
info.exactSolution.plot(label="Exact solution")
plt.title("Deconvolution 1D problem")
plt.legend()

<matplotlib.legend.Legend object at 0x7f58a85e05f0>

Setting up the prior#

We now need to define the prior distribution for the solution. In this case, we will use a Gaussian Markov Random Field (GMRF) prior. For more details on the GMRF prior, see the cuqi.distribution.GMRF documentation.

x = cuqi.distribution.GMRF(np.zeros(A.domain_dim), 200)

Setting up the likelihood#

We now need to define the likelihood. First let us take a look at the information provided by the test problem.

print(info.infoString)

Noise type: Additive Gaussian with std: 0.01

We see that the noise level is known and that the noise is Gaussian. We can use this information to define the likelihood. In this case, we will use a Gaussian distribution.

y = cuqi.distribution.Gaussian(A @ x, 0.01**2)

Bayesian problem (Joint distribution)#

After defining the prior and likelihood, we can now define the Bayesian problem. The Bayesian problem is defined by the joint distribution of the solution and the data. This can be seen when we print the Bayesian problem.

BP = cuqi.problem.BayesianProblem(y, x)

print(BP)

BayesianProblem with target:
 JointDistribution(
    Equation:
        p(y,x) = p(y|x)p(x)
    Densities:
        y ~ CUQI Gaussian. Conditioning variables ['x'].
        x ~ CUQI GMRF.
 )

Setting the data (posterior)#

Now to set the data, we need to call the set_data()

BP.set_data(y=y_data)

print(BP)

BayesianProblem with target:
 Posterior(
    Equation:
         p(x|y) ∝ L(x|y)p(x)
    Densities:
        y ~ CUQI Gaussian Likelihood function. Parameters ['x'].
        x ~ CUQI GMRF.
 )

Sampling from the posterior#

We can then use the automatic sampling method to sample from the posterior distribution.

samples = BP.sample_posterior(1000)

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!! Automatic sampler selection is a work-in-progress. !!!
!!!       Always validate the computed results.        !!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!  Using samplers from cuqi.sampler  !!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Using cuqi.sampler LinearRTO sampler.
burn-in: 20%

Warmup:   0%|          | 0/200 [00:00<?, ?it/s]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:   0%|          | 0/200 [00:00<?, ?it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  19%|█▉        | 38/200 [00:00<00:00, 377.46it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  38%|███▊      | 76/200 [00:00<00:00, 378.24it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  57%|█████▋    | 114/200 [00:00<00:00, 377.17it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  76%|███████▌  | 152/200 [00:00<00:00, 377.92it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup:  95%|█████████▌| 190/200 [00:00<00:00, 377.32it/s, acc rate: 100.00%]
Warmup: 100%|██████████| 200/200 [00:00<00:00, 377.51it/s, acc rate: 100.00%]

Sample:   0%|          | 0/1000 [00:00<?, ?it/s]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   0%|          | 0/1000 [00:00<?, ?it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   4%|▍         | 39/1000 [00:00<00:02, 381.38it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:   8%|▊         | 78/1000 [00:00<00:02, 380.42it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  12%|█▏        | 117/1000 [00:00<00:02, 380.54it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  16%|█▌        | 156/1000 [00:00<00:02, 380.04it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  20%|█▉        | 195/1000 [00:00<00:02, 379.63it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  23%|██▎       | 234/1000 [00:00<00:02, 379.87it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  27%|██▋       | 272/1000 [00:00<00:01, 379.82it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  31%|███       | 311/1000 [00:00<00:01, 380.22it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:00<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  35%|███▌      | 350/1000 [00:01<00:01, 380.58it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  39%|███▉      | 389/1000 [00:01<00:01, 380.44it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  43%|████▎     | 428/1000 [00:01<00:01, 380.47it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  47%|████▋     | 467/1000 [00:01<00:01, 380.52it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  51%|█████     | 506/1000 [00:01<00:01, 380.32it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  55%|█████▍    | 545/1000 [00:01<00:01, 381.14it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  58%|█████▊    | 584/1000 [00:01<00:01, 381.26it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  62%|██████▏   | 623/1000 [00:01<00:00, 381.15it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  66%|██████▌   | 662/1000 [00:01<00:00, 380.49it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  70%|███████   | 701/1000 [00:01<00:00, 380.52it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:01<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  74%|███████▍  | 740/1000 [00:02<00:00, 380.76it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  78%|███████▊  | 779/1000 [00:02<00:00, 380.31it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  82%|████████▏ | 818/1000 [00:02<00:00, 380.43it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  86%|████████▌ | 857/1000 [00:02<00:00, 379.55it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  90%|████████▉ | 895/1000 [00:02<00:00, 379.57it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  93%|█████████▎| 933/1000 [00:02<00:00, 379.38it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample:  97%|█████████▋| 971/1000 [00:02<00:00, 379.06it/s, acc rate: 100.00%]
Sample: 100%|██████████| 1000/1000 [00:02<00:00, 380.09it/s, acc rate: 100.00%]
Elapsed time: 3.164634943008423

Plotting the results#

samples.plot_ci(exact=info.exactSolution)

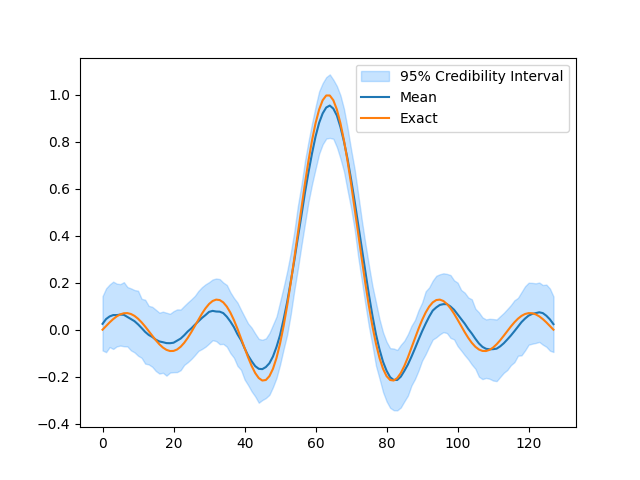
[<matplotlib.lines.Line2D object at 0x7f58a8575910>, <matplotlib.lines.Line2D object at 0x7f58a8575d00>, <matplotlib.collections.FillBetweenPolyCollection object at 0x7f58a63e45f0>]

Unknown noise level#

In the previous example, we assumed that we knew the noise level of the data. In many cases, this is not the case. If we do not know the noise level, we can use a Gamma distribution to model the noise level.

s = cuqi.distribution.Gamma(1, 1e-4)

Update likelihood with unknown noise level#

y = cuqi.distribution.Gaussian(A @ x, prec=lambda s: s)

Bayesian problem (Joint distribution)#

BP = cuqi.problem.BayesianProblem(y, x, s)

print(BP)

BayesianProblem with target:
 JointDistribution(
    Equation:
        p(y,x,s) = p(y|x,s)p(x)p(s)
    Densities:
        y ~ CUQI Gaussian. Conditioning variables ['x', 's'].
        x ~ CUQI GMRF.
        s ~ CUQI Gamma.
 )

Setting the data (posterior)#

BP.set_data(y=y_data)

print(BP)

BayesianProblem with target:
 JointDistribution(
    Equation:
        p(x,s|y) ∝ L(x,s|y)p(x)p(s)
    Densities:
        y ~ CUQI Gaussian Likelihood function. Parameters ['x', 's'].
        x ~ CUQI GMRF.
        s ~ CUQI Gamma.
 )

Sampling from the posterior#

samples = BP.sample_posterior(1000)

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!! Automatic sampler selection is a work-in-progress. !!!
!!!       Always validate the computed results.        !!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!  Using samplers from cuqi.sampler  !!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Using cuqi.sampler HybridGibbs sampler
burn-in: 20%

Automatically determined sampling strategy:
        x: LinearRTO (mcmc.sampler)
        s: Conjugate (mcmc.sampler)


Warmup:   0%|          | 0/200 [00:00<?, ?it/s]
Warmup:   8%|▊         | 16/200 [00:00<00:01, 157.61it/s]
Warmup:  16%|█▌        | 32/200 [00:00<00:01, 157.91it/s]
Warmup:  24%|██▍       | 48/200 [00:00<00:00, 157.85it/s]
Warmup:  32%|███▏      | 64/200 [00:00<00:00, 157.74it/s]
Warmup:  40%|████      | 80/200 [00:00<00:00, 157.38it/s]
Warmup:  48%|████▊     | 96/200 [00:00<00:00, 157.41it/s]
Warmup:  56%|█████▌    | 112/200 [00:00<00:00, 157.29it/s]
Warmup:  64%|██████▍   | 128/200 [00:00<00:00, 157.52it/s]
Warmup:  72%|███████▏  | 144/200 [00:00<00:00, 157.53it/s]
Warmup:  80%|████████  | 160/200 [00:01<00:00, 157.54it/s]
Warmup:  88%|████████▊ | 176/200 [00:01<00:00, 157.58it/s]
Warmup:  96%|█████████▌| 192/200 [00:01<00:00, 157.62it/s]
Warmup: 100%|██████████| 200/200 [00:01<00:00, 157.57it/s]

Sample:   0%|          | 0/1000 [00:00<?, ?it/s]
Sample:   2%|▏         | 16/1000 [00:00<00:06, 157.57it/s]
Sample:   3%|▎         | 32/1000 [00:00<00:06, 157.41it/s]
Sample:   5%|▍         | 48/1000 [00:00<00:06, 157.53it/s]
Sample:   6%|▋         | 64/1000 [00:00<00:05, 157.60it/s]
Sample:   8%|▊         | 80/1000 [00:00<00:05, 157.80it/s]
Sample:  10%|▉         | 96/1000 [00:00<00:05, 157.64it/s]
Sample:  11%|█         | 112/1000 [00:00<00:05, 157.50it/s]
Sample:  13%|█▎        | 128/1000 [00:00<00:05, 157.63it/s]
Sample:  14%|█▍        | 144/1000 [00:00<00:05, 157.71it/s]
Sample:  16%|█▌        | 160/1000 [00:01<00:05, 157.57it/s]
Sample:  18%|█▊        | 176/1000 [00:01<00:05, 157.68it/s]
Sample:  19%|█▉        | 192/1000 [00:01<00:05, 157.82it/s]
Sample:  21%|██        | 208/1000 [00:01<00:05, 157.58it/s]
Sample:  22%|██▏       | 224/1000 [00:01<00:04, 157.50it/s]
Sample:  24%|██▍       | 240/1000 [00:01<00:04, 157.35it/s]
Sample:  26%|██▌       | 256/1000 [00:01<00:04, 157.17it/s]
Sample:  27%|██▋       | 272/1000 [00:01<00:04, 157.12it/s]
Sample:  29%|██▉       | 288/1000 [00:01<00:04, 157.33it/s]
Sample:  30%|███       | 304/1000 [00:01<00:04, 157.33it/s]
Sample:  32%|███▏      | 320/1000 [00:02<00:04, 157.11it/s]
Sample:  34%|███▎      | 336/1000 [00:02<00:04, 156.76it/s]
Sample:  35%|███▌      | 352/1000 [00:02<00:04, 156.51it/s]
Sample:  37%|███▋      | 368/1000 [00:02<00:04, 156.80it/s]
Sample:  38%|███▊      | 384/1000 [00:02<00:03, 156.93it/s]
Sample:  40%|████      | 400/1000 [00:02<00:03, 156.54it/s]
Sample:  42%|████▏     | 416/1000 [00:02<00:03, 156.42it/s]
Sample:  43%|████▎     | 432/1000 [00:02<00:03, 156.38it/s]
Sample:  45%|████▍     | 448/1000 [00:02<00:03, 156.56it/s]
Sample:  46%|████▋     | 464/1000 [00:02<00:03, 156.45it/s]
Sample:  48%|████▊     | 480/1000 [00:03<00:03, 156.41it/s]
Sample:  50%|████▉     | 496/1000 [00:03<00:03, 156.68it/s]
Sample:  51%|█████     | 512/1000 [00:03<00:03, 156.85it/s]
Sample:  53%|█████▎    | 528/1000 [00:03<00:03, 156.91it/s]
Sample:  54%|█████▍    | 544/1000 [00:03<00:02, 156.92it/s]
Sample:  56%|█████▌    | 560/1000 [00:03<00:02, 157.20it/s]
Sample:  58%|█████▊    | 576/1000 [00:03<00:02, 156.29it/s]
Sample:  59%|█████▉    | 592/1000 [00:03<00:02, 156.14it/s]
Sample:  61%|██████    | 608/1000 [00:03<00:02, 156.80it/s]
Sample:  62%|██████▏   | 624/1000 [00:03<00:02, 157.07it/s]
Sample:  64%|██████▍   | 640/1000 [00:04<00:02, 157.42it/s]
Sample:  66%|██████▌   | 656/1000 [00:04<00:02, 157.92it/s]
Sample:  67%|██████▋   | 672/1000 [00:04<00:02, 157.75it/s]
Sample:  69%|██████▉   | 688/1000 [00:04<00:01, 157.80it/s]
Sample:  70%|███████   | 704/1000 [00:04<00:01, 157.95it/s]
Sample:  72%|███████▏  | 720/1000 [00:04<00:01, 158.32it/s]
Sample:  74%|███████▎  | 736/1000 [00:04<00:01, 158.25it/s]
Sample:  75%|███████▌  | 752/1000 [00:04<00:01, 158.43it/s]
Sample:  77%|███████▋  | 768/1000 [00:04<00:01, 158.65it/s]
Sample:  78%|███████▊  | 784/1000 [00:04<00:01, 158.64it/s]
Sample:  80%|████████  | 800/1000 [00:05<00:01, 158.71it/s]
Sample:  82%|████████▏ | 816/1000 [00:05<00:01, 158.84it/s]
Sample:  83%|████████▎ | 832/1000 [00:05<00:01, 158.17it/s]
Sample:  85%|████████▍ | 848/1000 [00:05<00:00, 158.10it/s]
Sample:  86%|████████▋ | 864/1000 [00:05<00:00, 158.28it/s]
Sample:  88%|████████▊ | 880/1000 [00:05<00:00, 158.49it/s]
Sample:  90%|████████▉ | 896/1000 [00:05<00:00, 158.32it/s]
Sample:  91%|█████████ | 912/1000 [00:05<00:00, 158.10it/s]
Sample:  93%|█████████▎| 928/1000 [00:05<00:00, 158.11it/s]
Sample:  94%|█████████▍| 944/1000 [00:05<00:00, 158.00it/s]
Sample:  96%|█████████▌| 960/1000 [00:06<00:00, 158.13it/s]
Sample:  98%|█████████▊| 976/1000 [00:06<00:00, 158.34it/s]
Sample:  99%|█████████▉| 992/1000 [00:06<00:00, 158.10it/s]
Sample: 100%|██████████| 1000/1000 [00:06<00:00, 157.53it/s]
Elapsed time: 7.6240222454071045

Plotting the results#

Let is first look at the estimated noise level and compare it with the true noise level

samples["s"].plot_trace(exact=1/0.01**2)

array([[<Axes: title={'center': 's'}>, <Axes: title={'center': 's'}>]],
      dtype=object)

We see that the estimated noise level is close to the true noise level. Let’s now look at the estimated solution

samples["x"].plot_ci(exact=info.exactSolution)

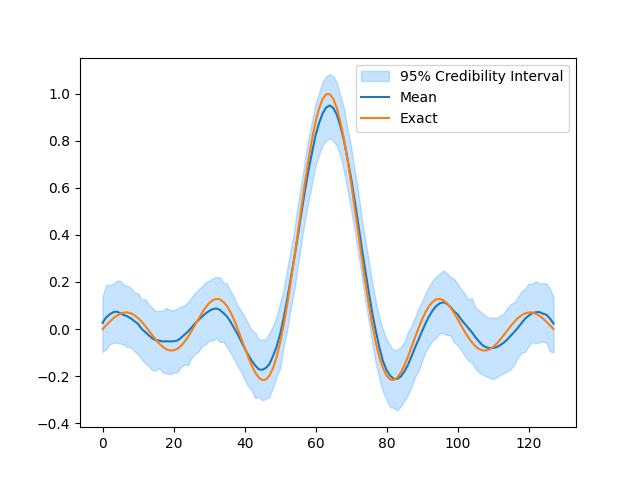
[<matplotlib.lines.Line2D object at 0x7f58a85e0f20>, <matplotlib.lines.Line2D object at 0x7f58a85e2840>, <matplotlib.collections.FillBetweenPolyCollection object at 0x7f58a6332c30>]

We can even plot traces of “x” for a few cases and compare

samples["x"].plot_trace(exact=info.exactSolution)

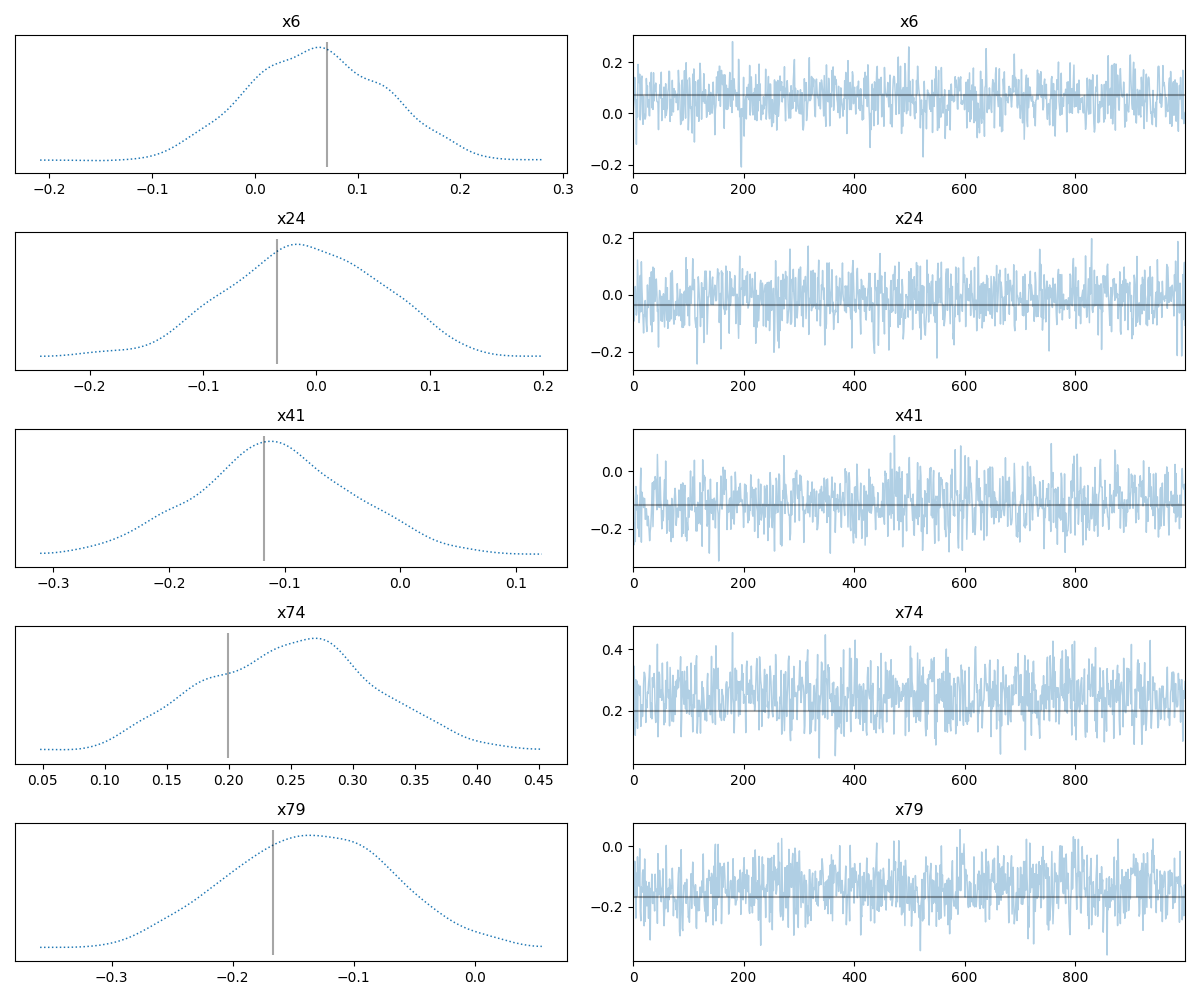
x32, x32, x38, x38, x65, x65, x79, x79, x106, x106

Selecting 5 randomly chosen variables

array([[<Axes: title={'center': 'x32'}>, <Axes: title={'center': 'x32'}>],
       [<Axes: title={'center': 'x38'}>, <Axes: title={'center': 'x38'}>],
       [<Axes: title={'center': 'x65'}>, <Axes: title={'center': 'x65'}>],
       [<Axes: title={'center': 'x79'}>, <Axes: title={'center': 'x79'}>],
       [<Axes: title={'center': 'x106'}>,
        <Axes: title={'center': 'x106'}>]], dtype=object)

And finally we note that the UQ method does this analysis automatically and shows a selected number of plots

BP.UQ(exact={"x": info.exactSolution, "s": 1/0.01**2})

Computing 1000 samples
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!! Automatic sampler selection is a work-in-progress. !!!
!!!       Always validate the computed results.        !!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!  Using samplers from cuqi.sampler  !!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Using cuqi.sampler HybridGibbs sampler
burn-in: 20%

Automatically determined sampling strategy:
        x: LinearRTO (mcmc.sampler)
        s: Conjugate (mcmc.sampler)


Warmup:   0%|          | 0/200 [00:00<?, ?it/s]
Warmup:   8%|▊         | 16/200 [00:00<00:01, 154.80it/s]
Warmup:  16%|█▌        | 32/200 [00:00<00:01, 155.90it/s]
Warmup:  24%|██▍       | 48/200 [00:00<00:00, 156.16it/s]
Warmup:  32%|███▏      | 64/200 [00:00<00:00, 156.69it/s]
Warmup:  40%|████      | 80/200 [00:00<00:00, 156.88it/s]
Warmup:  48%|████▊     | 96/200 [00:00<00:00, 156.85it/s]
Warmup:  56%|█████▌    | 112/200 [00:00<00:00, 156.88it/s]
Warmup:  64%|██████▍   | 128/200 [00:00<00:00, 156.78it/s]
Warmup:  72%|███████▏  | 144/200 [00:00<00:00, 156.40it/s]
Warmup:  80%|████████  | 160/200 [00:01<00:00, 156.33it/s]
Warmup:  88%|████████▊ | 176/200 [00:01<00:00, 156.64it/s]
Warmup:  96%|█████████▌| 192/200 [00:01<00:00, 156.84it/s]
Warmup: 100%|██████████| 200/200 [00:01<00:00, 156.60it/s]

Sample:   0%|          | 0/1000 [00:00<?, ?it/s]
Sample:   2%|▏         | 16/1000 [00:00<00:06, 156.82it/s]
Sample:   3%|▎         | 32/1000 [00:00<00:06, 156.76it/s]
Sample:   5%|▍         | 48/1000 [00:00<00:06, 156.51it/s]
Sample:   6%|▋         | 64/1000 [00:00<00:05, 156.77it/s]
Sample:   8%|▊         | 80/1000 [00:00<00:05, 156.90it/s]
Sample:  10%|▉         | 96/1000 [00:00<00:05, 156.88it/s]
Sample:  11%|█         | 112/1000 [00:00<00:05, 156.74it/s]
Sample:  13%|█▎        | 128/1000 [00:00<00:05, 156.72it/s]
Sample:  14%|█▍        | 144/1000 [00:00<00:05, 156.50it/s]
Sample:  16%|█▌        | 160/1000 [00:01<00:05, 156.61it/s]
Sample:  18%|█▊        | 176/1000 [00:01<00:05, 156.90it/s]
Sample:  19%|█▉        | 192/1000 [00:01<00:05, 157.22it/s]
Sample:  21%|██        | 208/1000 [00:01<00:05, 157.47it/s]
Sample:  22%|██▏       | 224/1000 [00:01<00:04, 157.46it/s]
Sample:  24%|██▍       | 240/1000 [00:01<00:04, 156.07it/s]
Sample:  26%|██▌       | 256/1000 [00:01<00:04, 156.51it/s]
Sample:  27%|██▋       | 272/1000 [00:01<00:04, 156.67it/s]
Sample:  29%|██▉       | 288/1000 [00:01<00:04, 157.25it/s]
Sample:  30%|███       | 304/1000 [00:01<00:04, 157.33it/s]
Sample:  32%|███▏      | 320/1000 [00:02<00:04, 157.28it/s]
Sample:  34%|███▎      | 336/1000 [00:02<00:04, 157.57it/s]
Sample:  35%|███▌      | 352/1000 [00:02<00:04, 157.77it/s]
Sample:  37%|███▋      | 368/1000 [00:02<00:04, 157.78it/s]
Sample:  38%|███▊      | 384/1000 [00:02<00:03, 157.71it/s]
Sample:  40%|████      | 400/1000 [00:02<00:03, 158.10it/s]
Sample:  42%|████▏     | 416/1000 [00:02<00:03, 158.26it/s]
Sample:  43%|████▎     | 432/1000 [00:02<00:03, 158.21it/s]
Sample:  45%|████▍     | 448/1000 [00:02<00:03, 158.30it/s]
Sample:  46%|████▋     | 464/1000 [00:02<00:03, 158.59it/s]
Sample:  48%|████▊     | 480/1000 [00:03<00:03, 158.43it/s]
Sample:  50%|████▉     | 496/1000 [00:03<00:03, 158.54it/s]
Sample:  51%|█████     | 512/1000 [00:03<00:03, 158.46it/s]
Sample:  53%|█████▎    | 528/1000 [00:03<00:02, 158.34it/s]
Sample:  54%|█████▍    | 544/1000 [00:03<00:02, 158.49it/s]
Sample:  56%|█████▌    | 560/1000 [00:03<00:02, 158.55it/s]
Sample:  58%|█████▊    | 576/1000 [00:03<00:02, 158.65it/s]
Sample:  59%|█████▉    | 592/1000 [00:03<00:02, 158.57it/s]
Sample:  61%|██████    | 608/1000 [00:03<00:02, 158.46it/s]
Sample:  62%|██████▏   | 624/1000 [00:03<00:02, 158.57it/s]
Sample:  64%|██████▍   | 640/1000 [00:04<00:02, 158.49it/s]
Sample:  66%|██████▌   | 656/1000 [00:04<00:02, 158.45it/s]
Sample:  67%|██████▋   | 672/1000 [00:04<00:02, 158.56it/s]
Sample:  69%|██████▉   | 688/1000 [00:04<00:01, 158.54it/s]
Sample:  70%|███████   | 704/1000 [00:04<00:01, 158.49it/s]
Sample:  72%|███████▏  | 720/1000 [00:04<00:01, 158.33it/s]
Sample:  74%|███████▎  | 736/1000 [00:04<00:01, 158.51it/s]
Sample:  75%|███████▌  | 752/1000 [00:04<00:01, 158.63it/s]
Sample:  77%|███████▋  | 768/1000 [00:04<00:01, 158.70it/s]
Sample:  78%|███████▊  | 784/1000 [00:04<00:01, 158.84it/s]
Sample:  80%|████████  | 800/1000 [00:05<00:01, 158.60it/s]
Sample:  82%|████████▏ | 816/1000 [00:05<00:01, 158.71it/s]
Sample:  83%|████████▎ | 832/1000 [00:05<00:01, 158.54it/s]
Sample:  85%|████████▍ | 848/1000 [00:05<00:00, 158.15it/s]
Sample:  86%|████████▋ | 864/1000 [00:05<00:00, 158.18it/s]
Sample:  88%|████████▊ | 880/1000 [00:05<00:00, 158.03it/s]
Sample:  90%|████████▉ | 896/1000 [00:05<00:00, 156.92it/s]
Sample:  91%|█████████ | 912/1000 [00:05<00:00, 157.09it/s]
Sample:  93%|█████████▎| 928/1000 [00:05<00:00, 157.51it/s]
Sample:  94%|█████████▍| 944/1000 [00:05<00:00, 157.60it/s]
Sample:  96%|█████████▌| 960/1000 [00:06<00:00, 157.31it/s]
Sample:  98%|█████████▊| 976/1000 [00:06<00:00, 157.77it/s]
Sample:  99%|█████████▉| 992/1000 [00:06<00:00, 157.64it/s]
Sample: 100%|██████████| 1000/1000 [00:06<00:00, 157.82it/s]
Elapsed time: 7.620683670043945
Plotting results

CUQIpy JointSamples Dict:
-------------------------

Keys:
 ['x', 's']

Ns (number of samples):
 {'x': 1000, 's': 1000}

Geometry:
 {'x': _DefaultGeometry1D[128], 's': _DefaultGeometry1D[1]}

Shape:
 {'x': (128, 1000), 's': (1, 1000)}

Total running time of the script: (0 minutes 19.285 seconds)

Gallery generated by Sphinx-Gallery

Uncertainty Quantification in one-dimensional deconvolution#

Setup#

Setting up the forward model#

Setting up the prior#

Setting up the likelihood#

Bayesian problem (Joint distribution)#

Setting the data (posterior)#

Sampling from the posterior#

Plotting the results#

Unknown noise level#

Update likelihood with unknown noise level#

Bayesian problem (Joint distribution)#

Setting the data (posterior)#

Sampling from the posterior#

Plotting the results#

This Page