Overview of CUQIpy

Table of Contents:¶

Note: some of the details mentioned here will make more sense after going through the next notebook that demonstrates how to use CUQIpy to solve a simple Bayesian inverse problem.

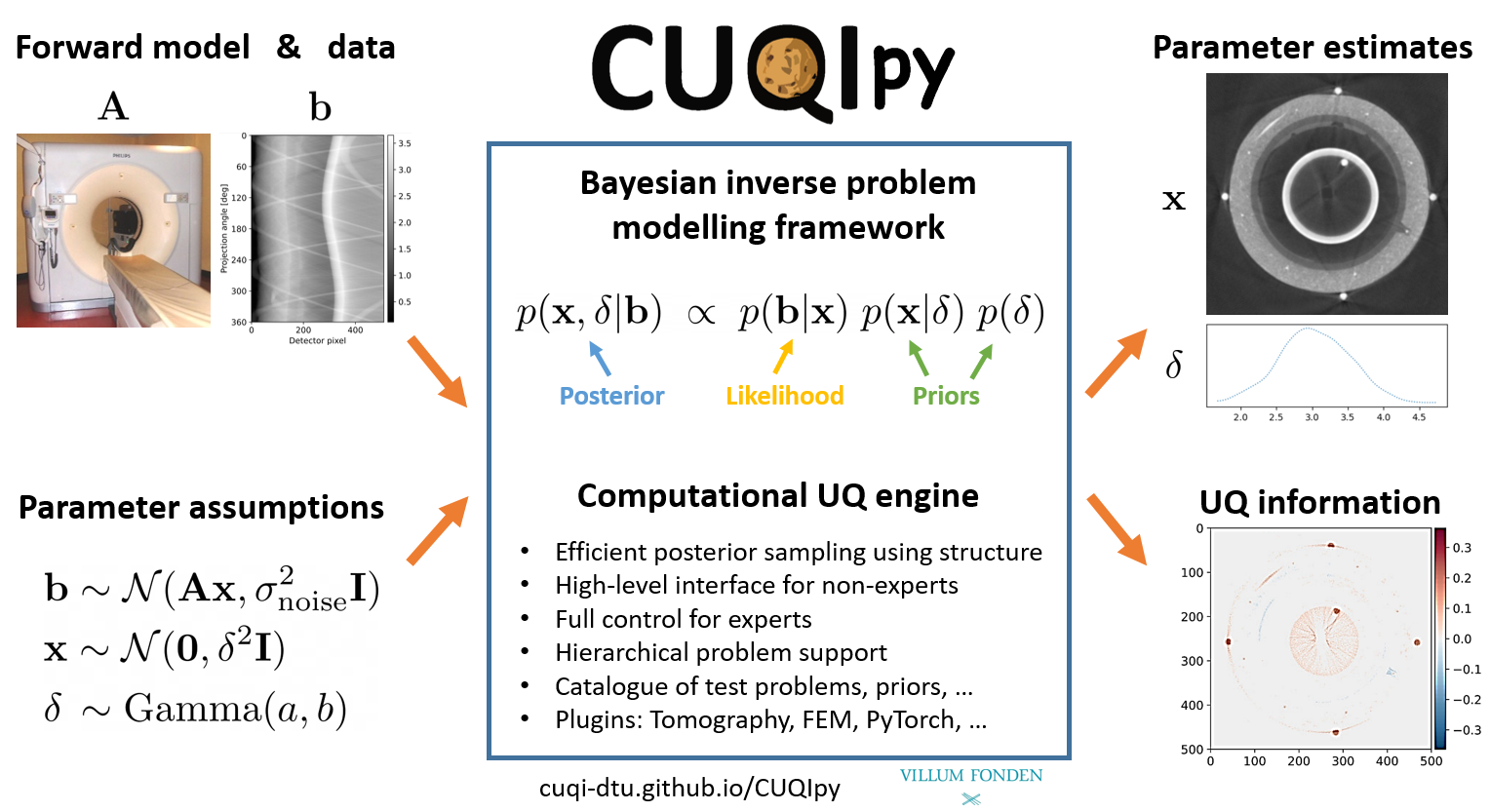
What is CUQIpy? ¶

CUQIpy is a Python package.
CUQIpy stands for Computational Uncertainty Quantification for Inverse Problems in Python.
CUQIpy provides a framework for solving inverse problems using Bayesian inference.
The framework enables:
- Modeling Bayesian inverse problems
- Solving Bayesian inverse problems using classical and advanced numerical tools
- Analyzing the solution of Bayesian inverse problems

Why CUQIpy? ¶

CUQIpy is built to address the need for:

A unified framework for solving Bayesian inverse problems across various scientific and engineering applications
A platform for modeling, solving and analyzing the solution of Bayesian inverse problems
A tool that can be used for both research and teaching
A tool that can be used by both beginners and advanced users
A tool that combines classical and advanced and scalable numerical methods for solving Bayesian inverse problems
A tool that is implemented purely in Python with minimal dependencies and can be easily maintained and integrated with other tools

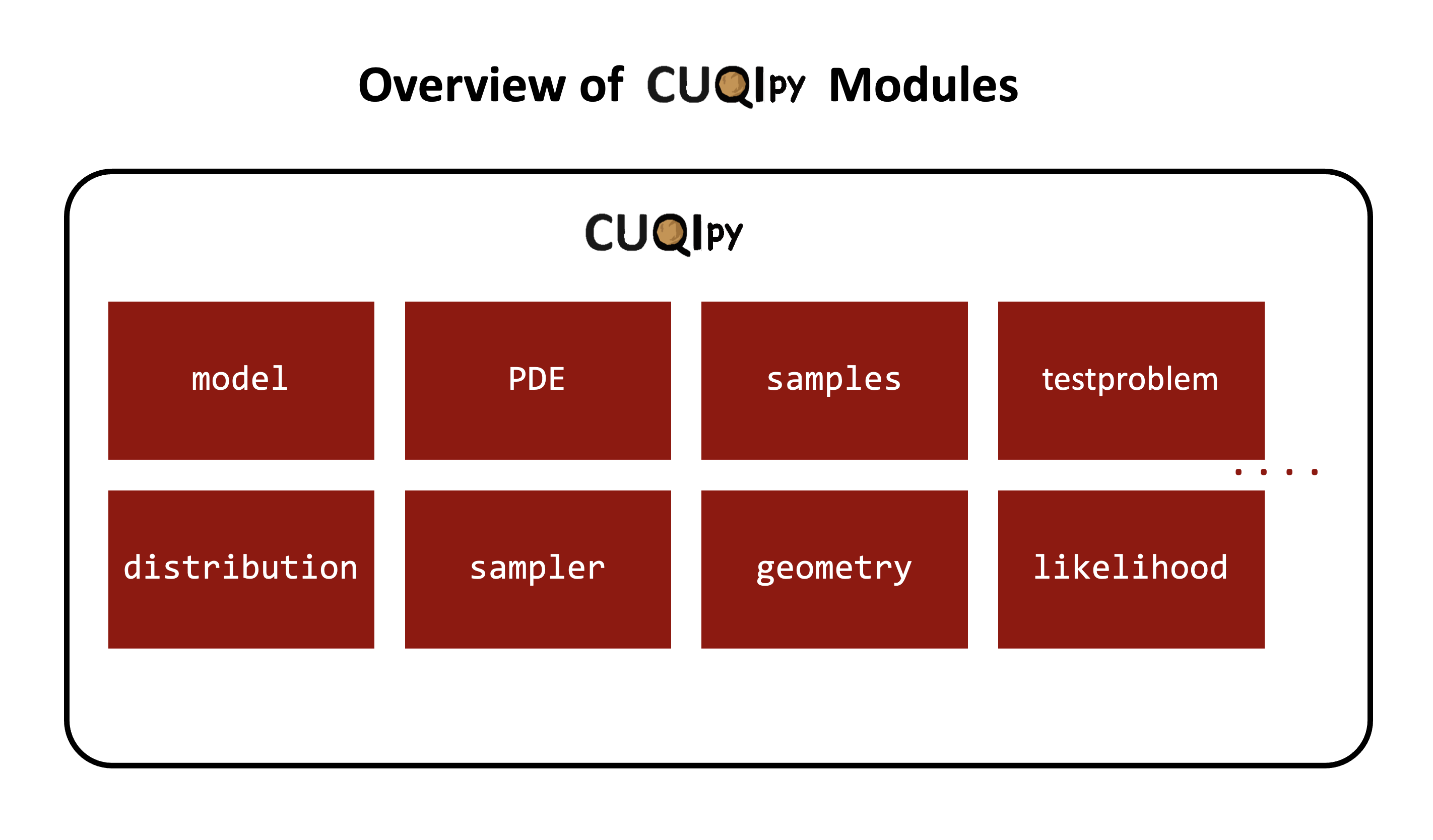
CUQIpy modules ¶

CUQIpy consists of many modules for modeling, solving, and analyzing Bayesian inverse problems.
These modules mostly correspond to typical components/tools needed for modeling and solving Bayesian inverse problems.
Each module contains classes and functions that are used to perform specific tasks.
Click here for an overview of the modules available in CUQIpy.

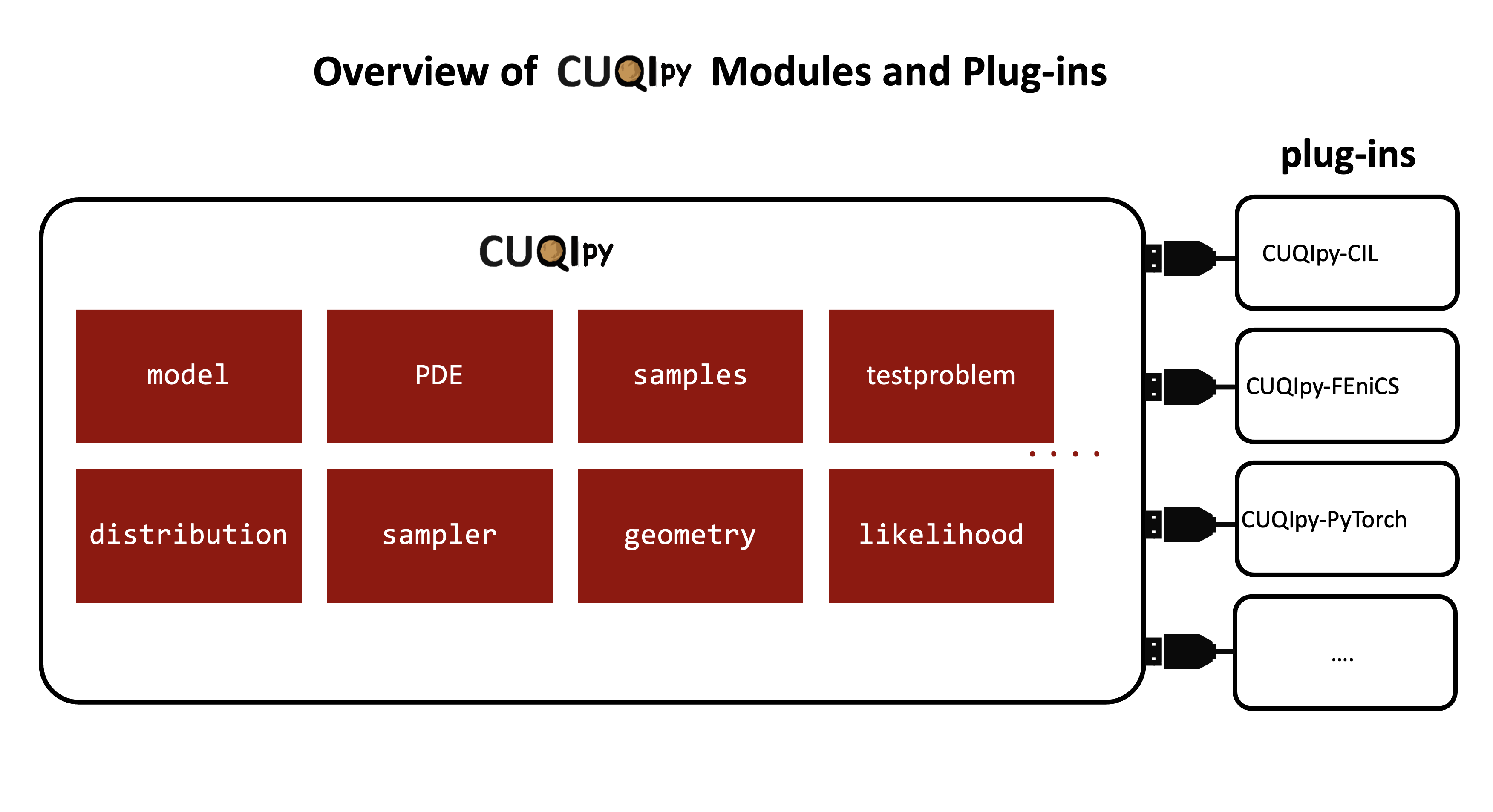
CUQIpy plugins ¶

In addition to the CUQIpy modules, CUQIpy also has plugins that extend the functionality of the framework.
These plugins allow integration of third-party software and tools with CUQIpy.
Click here to see the list of plugins available in CUQIpy.

CUQIpy design principles ¶

Provide simple and intuitive interface for users
Design for flexibility, extensibility, modularity, and maintainability
Accommodate both beginners and advanced users. e.g.,
- Provide a set of test problems to use for experimentation and prototyping
- Automatic sampler selection for a range of problems
- Enable advanced customization of the problem setup and solution
Aligning the modeling code with the mathematical formulation of the problem, e.g.,

Bayesian model:

\begin{align*} d &\sim \text{Gamma}(1, 10^{-4})\\ s &\sim \text{Gamma}(1, 10^{-4})\\ x &\sim \text{LMRF}(\mathbf{0}, d^{-1})\\ y &\sim \text{Gaussian}(\mathbf{A}\mathbf{x}, s^{-1}\mathbf{I})\\ p(d,s,x,y) &= p(d)p(s)p(x|d)p(y|x,s) \end{align*}

(1)

where $d^{-1}$ and $s$ are the precision parameters of the prior (the LMRF) and the data distribution (the Gaussian), respectively, $x$ is the unknown parameter, and $y$ is the data. $\mathbf{A}$ is the forward operator.

Bayesian model in CUQIpy:

d = Gamma(1, 1e-4)
s = Gamma(1, 1e-4)
x = LMRF(0, lambda d: 1/d)
y = Gaussian(A@x, lambda s: 1/s)
joint = JointDistribution(d, s, x, y)

See setting up a Bayesian model in CUQIpy in 4 steps here.